Aviation : 081 Principles Of Flight : Flight Mechanics : Question 1

What happens to the descent angle as an aircraft descends from FL400 to FL250 at constant Mach number then from FL250 to FL100 at constant CAS?

a. Increase, increase
b. Increase, constant
c. Decrease, decrease
d. Decrease, constant

Solution and explanation

* From FL400 to FL360 (M = constant):

During the descent through the stratosphere (FL400) to the tropopause (FL360) the temperature will be constant (-56,5°C) so the TAS at any fixed mach number will be constant.

In fact, the formula for the mach number (M) is

M = TAS / LSS

Local Speed of Sound (LSS) depends on the OAT (Outside Air Temperature)

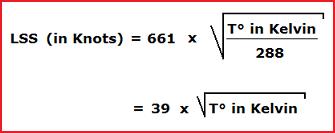
So if the outside air temperature remains constant, LSS is constant and at constant mach number the True Air Speed (TAS) will remain constant.

But as we descend at this constant TAS our CAS (Calibrated Air Speed) will increase (CAS = IAS if we neglect the position error of the static port; IAS = Indicated Air Speed).

In fact, the formula for dynamic pressure (q) is

q = 1/2 Rho TAS² = 1/2 Rho₀ EAS², (see Equivalent Air Speed)

and if you neglect the compressibility error below FL250, which is fine because of the low value of the mach number below that altitude, you can also say q = 1/2 Rho₀ CAS² (CAS = EAS if compressibility error is neglected) (see the difference between IAS, CAS, EAS and TAS and the formula for compressibility error).

Rho₀ = constant = air density at Sea Level in the International Standard Atmosphere (SL ISA) = 1,225 kg/m³. So because the density of the air, Rho, increases during the descent at constant TAS, then the CAS and the dynamic pressure (q) will be increasing too according to the formula hereabove.

However, the formula for the total drag is :

D = q S C_D

Therefore because the dynamic pressure q increases during the descent, then the drag D increases too.

If we do nothing, this increase in drag will cause the aircraft to decelerate. Assuming idle power is set, then to maintain constant mach we must prevent this increase in drag by pushing the nose down (by doing so, the weight component acting along the flight path will be increased and will balance the increase in drag). This will make our descent path steeper. So the descent angle will become more negative.

Another way to look at it is to remember that the formula for the angle of descent is

sin(angle of descent) = (D-T)/W

Drag minus thrust, divided by weight equals to the sine of the angle of descent.

But thrust is set to idle so T = 0 and D increases during the descent so we reach the same conclusion, the angle of descent increases.

* From FL360 to FL250 (M = constant):

During the constant mach descent from the tropopause (flight level 360) to the crossover altitude (flight level 250) the outside air temperature and LSS (local speed of sound) will both increase. So to maintain constant mach we must increase the TAS and the CAS (see the formulas studied hereabove). Once again this will be done by pushing the nose down. This will make the descent path steeper again.

Conclusion : throughout the constant mach part of the descent, from FL400 to FL250, the descent path will become steeper : the angle of descent increases.

* From FL250 to FL100 (CAS = constant):

If we do nothing during the constant CAS part of the descent (i.e below the crossover altitude) then the angle of attack will be constant. In fact, when flying at 1g (load factor = n = L/W = 1) and not in stall, then for a given weight there is only one possible CAS for each angle of attack. So if the CAS is maintained constant, then the angle of attack will remain constant too. This will produce constant drag.

In fact, as we look at the formula for drag :

D = 1/2 Rho₀ CAS² S C_D

Remark: to be 100% correct, the formula for drag should use the EAS instead of the CAS. However, below FL240 we can neglect the compressibility error and say that CAS is almost equal to EAS.

If the angle of attack remains constant then C_D is constant, and if CAS remains constant too then we may conclude that D is constant.

Sin(angle of descent) = (D – T)/W

Thrust is set to idle thus T = 0. Therefore if D is a constant then the angle of descent is a constant too.

But for our constant CAS descent we need to have a decreasing TAS (because Rho is increasing ; see formula for dynamic pressure hereabove). It may be tempting to think that we need to gradually pull the nose up to achieve this. But if we select a pitch angle that gives a drag force that is slightly greater than the component of weight acting down the flight path, then our TAS will decrease. If we select exactly the right pitch angle, the rate of deceleration will be just enough to give decrease TAS at such a rate that the CAS remains constant. Having selected this correct pitch angle we need to do nothing more to maintain constant CAS.

Conclusion : throughout the constant CAS part of the descent, from FL250 to FL100, our descent angle will be constant.

* Why do we make a descent at constant mach number and then at constant CAS ?

Before we answer that question let us study the different speed limitations of an airplane.

The speed of the aircraft is limited for different reasons.

- Maximum dynamic pressure ("q_max") :

The best parameter to represent the dynamic pressure of the airflow around an airplane is the EAS (Equivalent Air Speed). If the airplane flies too fast, which means at high EAS (or high TAS and high air density Rho) then the dynamic pressure on the aircraft is too high. Thus the aerodynamic forces acting on the different parts of the aircraft might break it (see the following formula for dynamic pressure : q = 1/2 Rho₀ EAS² = 1/2 Rho TAS²).

This is why an airplane has a maximum EAS permitted and you should never fly above that EAS. However it is presented to the pilot as an IAS on his air speed indicator (see the difference between IAS and EAS).

- Bird strike :

The constructor might also want to limit the speed of the airplane to make sure that a bird strike will not break the windshield or the wing for instance. Tests are conducted with fake birds of a certain mass and the maximum permitted speed is limited to ensure that the windshield will resist such a bird strike. Have a look at the damage a bird can cause to the wing or to the windscreen :

To avoid the severe damages caused by a too high dynamic pressure or a bird strike, the constructor will define a maximum speed called V_MO (Max Operating speed) or M_MO (Max Operating mach number). That max speed is shown to the pilot of a jet as an IAS (or CAS if corrected for the position error of the static port) on his Air Speed Indicator (ASI).

The position of the barber's pole (red and white) shows the value of V_MO on the Air Speed Indicator.

The pilot is flying close to VMO (white needle almost on the red and white barber's pole).

On small airplanes (light piston engine), V_MO does not exist but the constructor does determine a maximum speed which is called V_NE (Never Exceed speed). If you do fly above V_NE you might reach the maximum allowed dynamic pressure and break something on your airplane. Your aircraft might even suffer from flutter if you fly at a speed above V_NE (see our selection of footages about flutter)

- Undesired effect of a strong shockwave :

At a high mach number (let's say M = 0,86 for instance), the speed of the airflow on some parts of the wing will be supersonic eventhough the airplane is flying below the speed of sound (M < 1).

In a high transonic regime (0,75 < M < 1,2), a strong shockwave will appear on the wing and the static pressure (P_s) of the air behind the wave will increase sharply. This will establish an adverse pressure gradient and the boundary layer behind the shockwave will separate from the aerofoil causing a disturbed turbulent airflow impacting the fuselage, the vertical and horizontal stabilizer. This will generate what is called high speed buffet. Those buffets might cause an accelerated fatigue of the structure and be very uncomfortable for the pilots and passengers as well.

Also, at a high transonic regime, the airplane will undergo a high speed stall because the shockwave will have caused the separation of the boundary layer on an important portion of the wing chord.

High speed buffet will occur before the high speed stall. To avoid the onset of the high speed buffet, the constructor will define a Maximum Operating mach number : M_MO.

- Now let's answer the initial question : why do we make the descent at constant mach number till the crossover altitude and then we continue the descent at a constant CAS ?

If you look carefully at the formula for the mach number (M = TAS/LSS) and the formula for dynamic pressure, q = 1/2 Rho TAS² = 1/2 Rho₀ EAS² = 1/2 Rho₀ CAS² (CAS = EAS if compressibility error is neglected below FL250), you will observe that while descending at a high constant mach number close from M_MO, then TAS increases because LSS increases.

However Rho increases too during the descent, so CAS and q increase if M = constant. So when the airplane has reached an altitude around FL250 (= crossover altitude, usually between FL290 and FL240, it depends on the Outside Air Temperature), the airplane is at its max allowed EAS (or CAS if we neglect the compressibility error) and the V_MO indicated by the barber's pole shows an indicated air speed where the airplane is at the same time limited by the maximum dynamic pressure allowed and the high speed buffet. So the pilot must now continue the descent at a constant CAS close to the V_MO indicated at the crossover altitude. Doing so, the mach number will decrease. In fact, flying at a constant CAS during a descent means that we fly at constant q but Rho is increasing so TAS must be decreasing to maintain a constant CAS (or constant q). Temperature is also increasing during the descent so LSS is increasing and Mach number is decreasing.

This is why descending at a constant CAS slightly below V_MO, under the crossover altitude, maintains the aircraft slightly below the maximum dynamic pressure and leads the airplane away from high speed buffet because the mach number is decreasing.