Aviation : 081 Principles Of Flight : Flight Mechanics : Question 2

You are flying on a standard day (ISA atmosphere) at flight level 200 and the mach number of your aircraft is M = 0,82. What is the value of the true air speed (TAS), the Equivalent Air Speed (EAS) and the Calibrated Air Speed (CAS) of your airplane ?

Solution and explanation

The formula for the mach number (M) is

M = TAS/LSS

and

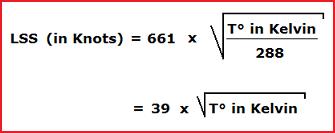
LSS is the Local Speed of Sound.

TAS is the True Air Speed of the airplane.

The temperature in Kelvin is the Outside Air Temperature (OAT) in degrees Celsius plus 273.

T° in Kelvin = °C + 273 (e.g. 20 °C = 293 K)

We also know that in a standard atmosphere (ISA, International Standard Atmosphere) at sea level (SL), the temperature is 15°C and the pressure is 1013 hPa. Then the temperature deacreases during the climb by 2°C per 1000 feet.

* T°_SL-ISA = 15°C

* Atmospheric Pressure_SL-ISA = 1013 hPa

* T° Lapse rate_ISA = -2°C / 1000 feet or -6,5°C / 1000 meters

So what is the temperature at FL200 (which is 20000 feet above the 1013 hPa isobar) ?

15°C - 20000x(2°C/1000 ft) = 15 - 40 = -25°C = Outside Air Temperature (OAT) at FL200

What is the value of the local speed of sound (LSS) at FL200 ?

LSS = 39 x square root[-25°C + 273] = 614 Kt

We can now work out the value of the TAS.

TAS = M x LSS = 0,82 x 614 = 503 kt

How are we going to find the value of the EAS now ? First, have a look at the following graphs.

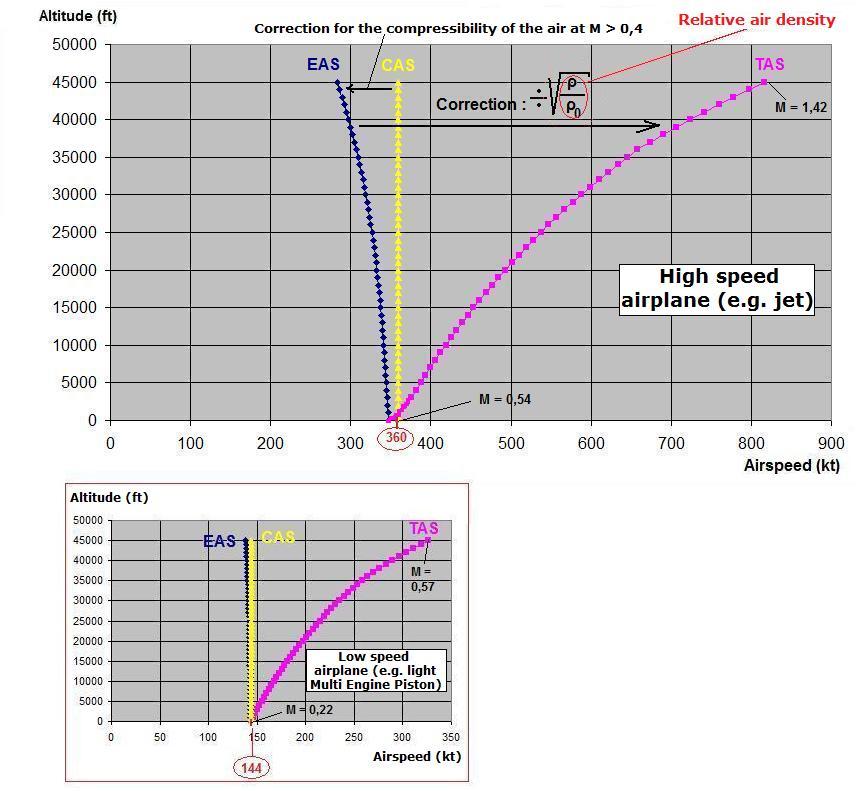
IAS : the Indicated Air Speed is the speed red by the pilot on the air speed indicator. We suppose that the IAS is corrected for instrument errors.

CAS : the Calibrated Air Speed (or RAS, Rectified Air Speed) is the IAS corrected for the position error of the static port. That position error is greater when you are flying slow, with flaps down, or when the airplane is in a side slip or a skid.

EAS : the Equivalent Air Speed is the CAS corrected for the error due to the compressibility of the air. That compressibility error is very small when you are flying at a mach number below 0,4. However above M = 0,4 the compressibility error becomes quite important. For instance, if you fly at an IAS of 200 Kt at FL200, the mach number of your airplane is slightly above 0,4. So for a small twin piston (MEP, multi engine piston) flying low and slow, the compressibility error is negligible. This is why there is almost no difference between the CAS and the EAS on the second graph. However for a jet, flying fast and high, it is another story and as you can see on the first graph, during the climb at a constant CAS, the difference between the CAS and the EAS increases constantly and so does the compressibility error.

Compressibility error = square root[1 + M²/4 + M⁴/40 + M⁶/1600]

Relationship between CAS and EAS :
CAS = EAS x square root[1 + M²/4 + M⁴/40 + M⁶/1600]

So as you can see in the formula, the higher the mach number, the bigger the compressibility error.

Remark : the compressibility error would not exist on the air speed indicator if it had been built based on Bernoulli's principle modified as follows :
Pt = Ps + q + "additional pressure due to compressibility of the air".

TAS : the True Air Speed is the EAS corrected for the relative density of the air. The relative density of the air is Rho/Rho₀, where Rho is the real air density at the flight level considered. While Rho₀ = 1,225 kg/m³, which is the value of the air density at Sea Level in a standard atmosphere (SL ISA). As you can see on the graph, if your airplane is flying on a standard day at SL, then TAS = EAS. However if the airplane flies higher than SL, even in a standard atmosphere, then TAS is greater than EAS because the real air density (Rho) is no longer 1,225 kg/m³ (Rho decreases with increasing altitude).

What can you remember from those graphs ?

1. The best parameter to represent the dynamic pressure (q) around the airplane is the EAS. However, if you fly at a speed below M = 0,4 then CAS represents the dynamic pressure with enough accuracy. If your airplane is not in a sideslip, a skid or close from stall, you can neglect the position error and say that IAS represents also quite well the dynamic pressure at M < 0,4.

2. At SL ISA, for all mach numbers, TAS is exactly equal to EAS.

3. At SL ISA, for M < 0,4, TAS is almost equal to CAS.

4. At SL ISA, for M < 0,4, EAS is almost equal to CAS.

5. If you climb at constant dynamic pressure, which means at constant EAS, then CAS is increasing and TAS as well.

6. If you climb at constant CAS (so at constant IAS), TAS increases also. You will arrive at your destination faster !

Let us know compute the value of EAS.

We found that TAS = 503 kt. We can now find the EAS as follows :

Dynamic pressure (q) = 1/2 Rho₀ EAS² = 1/2 Rho TAS²

I use the formula for dynamic pressure hereabove to find that
EAS = TAS x square root[Rho/Rho₀]

I now take the table of the standard atmosphere to find the air density Rho at FL200. I find Rho_FL200 = 0,6528 kg/m³.

Therefore, at FL200, EAS = 503 x square root (0,6528/1,225) = 367 Kt

We can now find the CAS using the formula
CAS = EAS x square root[1 + M²/4 + M⁴/40 + M⁶/1600]

CAS = 367 x square root[1 + 0,82²/4 + 0,82⁴/40 + 0,82⁶/1600] = 399 Kt

* Summary of the answers found :

TAS = 503 Kt ; EAS = 367 Kt ; CAS = 399 Kt.